
© FreeRangeStock
Maths formulas hold the secret of the universe. And lets explore best of them.
Mathematics is often described as the language of the universe. From the ancient pyramids of Egypt to the modern smartphones in our pockets, math has been a foundational pillar of human advancement. Among its vast library of theorems, rules, and equations, certain mathematical formulas are used more frequently than others — in classrooms, research, engineering, finance, and even daily life. Here are the 6 most used mathematics formulas, the geniuses who developed or popularized them, when they came into play, and why they remain essential in our world today.
Similar Titles For Above List
- Maths Formulas Ruling The World
- Maths Formulas and Their Origins
1 . The Pythagorean Theorem
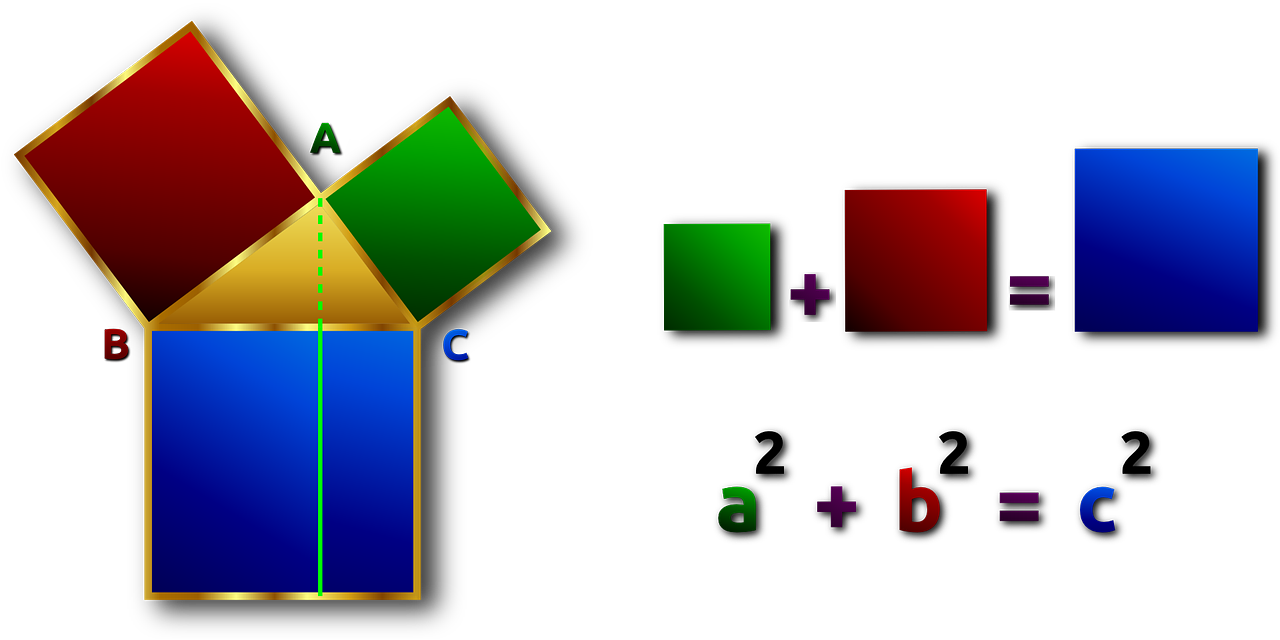
© Needpix.com
The Pythagorean Theorem : The Triangle and Its Angles Study
📌 Formula: a² + b² = c² 📜 Origin: Who: Pythagoras of Samos (c. 570–495 BCE), Greek mathematician and philosopher. When: Around 500 BCE, though earlier records exist in Babylonian mathematics.
🔍 Why It’s Important:
This fundamental geometric formula calculates the relationship between the three sides of a right-angled triangle. It’s used across construction, physics, navigation, and computer graphics.
🧠 Real-World Application:
Surveyors use it to determine land boundaries.
GPS systems rely on it to triangulate locations.
Architects use it when designing buildings and bridges.
2 . Quadratic Formula

© Wikipedia
The Curves All Mathematicians Loves
📌 Formula: x = (-b ± √(b² - 4ac)) / 2a 📜 Origin: Who: Brahmagupta (598–668 CE), an Indian mathematician, made one of the earliest known systematic uses. Modern Form: Developed during the Islamic Golden Age and standardized in the 17th century.
🔍 Why It’s Important:
This formula solves any quadratic equation of the form ax² + bx + c = 0. It’s vital in algebra and appears in physics, engineering, and economics problems.
🧠 Real-World Application:
Used in projectile motion equations.
Financial analysts use it in modeling investment scenarios.
Engineers use it in system design and optimization.
Read More..
Check out freeCodeCamp.
Check out freeCodeCamp.
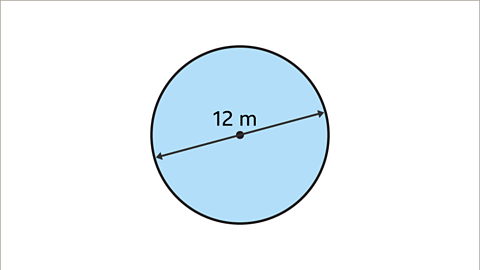
3 . Area of a Circle
© BBC
Life Or Maths : Both Have Circles
📌 Formula: A = πr² 📜 Origin: Who: Archimedes (c. 287 BCE – c. 212 BCE), Greek mathematician. When: Around 250 BCE, though the concept of π was used earlier in Egypt and Babylon.
🔍 Why It’s Important:
This elegant formula calculates the space inside a circle. Understanding π (pi), a mathematical constant, is key in advanced geometry and calculus.
🧠 Real-World Application:
Used to design wheels, gears, and disks.
Helps calculate coverage area (like a circular garden or pool).
Crucial in signal processing and electronics.
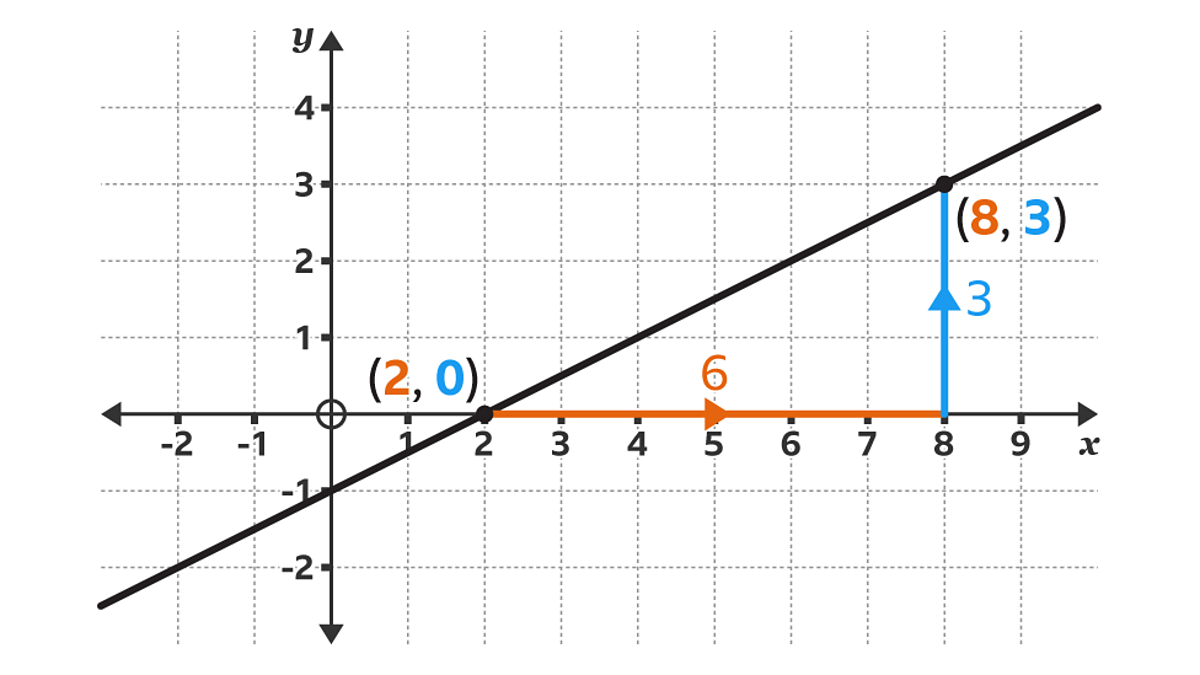
4 . The Slope Formula (Gradient)
© BBC
Slope Of Co-Ordinates
📌 Formula: m = (y₂ - y₁) / (x₂ - x₁) 📜 Origin: Who: René Descartes (1596–1650), father of analytical geometry. When: Early 17th century.
🔍 Why It’s Important:
This formula calculates the steepness or incline of a line, helping us understand the rate of change between two points on a Cartesian plane.
🧠 Real-World Application:
Used in economics to calculate cost and revenue change.
In geography, it's used to determine the gradient of slopes or roads.
In data science, slope helps understand trends in scatter plots and regression models.
5 . Euler’s Formula (for complex numbers)

© Wikipedia
Formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function.
📌 Formula: e^(ix) = cos(x) + i·sin(x) 📜 Origin: Who: Leonhard Euler (1707–1783), Swiss mathematician. When: 1740s.
🔍 Why It’s Important:
This is one of the most beautiful formulas in mathematics, linking five key mathematical constants: e, i, π, 1, and 0. It's heavily used in fields involving wave functions, quantum mechanics, and electrical engineering.
🧠 Real-World Application:
Signal processing and telecommunications.
Describing oscillations and waves in physics.
Modeling alternating current (AC) circuits.
6 . The Derivative (Basic Calculus Rule)

© Wikipedia
Derivative of a constant is zero, a constant can be factored out, and the derivative of a sum is the sum of the derivatives
📌 Formula: f'(x) = lim (h → 0) [(f(x + h) - f(x)) / h] 📜 Origin: Who: Independently developed by Isaac Newton and Gottfried Wilhelm Leibniz in the late 1600s. When: Around 1666–1684.
🔍 Why It’s Important:
This formula measures the rate of change or slope of a function at any point — a core idea in calculus.
🧠 Real-World Application:
Predicts population growth, speed, and acceleration.
Used in optimization problems across business and manufacturing.
Fundamental in machine learning models and AI algorithms.
# . Extra Mentions
7 . Distance Formula (in Coordinate Geometry)
📌 Formula:
D = √[(x₂ - x₁)² + (y₂ - y₁)²]
📜 Origin:
Derived from the Pythagorean Theorem.
Popularized in the study of analytic geometry by René Descartes in the 17th century.
🔍 Why It’s Important:
This formula calculates the straight-line distance between two points in a 2D space. It's a foundational concept in geometry and physics.
🧠 Real-World Application:
Used in mapping systems and navigation apps to measure distance between two locations.
In video games and animation, it calculates object collisions or distances between characters.
In data clustering (like k-means), it measures how far points are from centroids.
8 . Simple Interest Formula
📌 Formula:
SI = (P × R × T) / 100
Where:
SI = Simple Interest
P = Principal Amount
R = Rate of Interest
T = Time (in years)
📜 Origin:
Roots in Babylonian and Roman financial practices.
Widely formalized and used in modern banking systems.
🔍 Why It’s Important:
This formula is essential for understanding how money grows over time when borrowed or invested, without compounding.
🧠 Real-World Application:
Used in banking and finance to calculate interest on loans, savings accounts, and bonds.
Applied in contracts and legal agreements involving fixed returns.
. Conclusion
Whether you’re a student just beginning your journey or a professional applying these rules daily, understanding these formulas connects you to centuries of innovation and opens doors to solving the problems of tomorrow. And that’s the real magic of math — it’s timeless, logical, and always evolving. So next time you solve an equation, remember: you’re not just crunching numbers — you’re speaking the same language as the architects of modern civilization.
Keywords
math formulas
most used math formulas
popular math equations
mathematics in real life
Pythagorean theorem
quadratic formula
area of circle
slope formula
Euler's formula
derivative formula
Archimedes
Newton
algebra basics
calculus in daily life
formula origin
who invented formulas
famous math discoveries
school math formulas
real world math
essential math equations
SOURCE"s & REFERENCE"s
- [1]
britannica.com
https://www.britannica.com/science/Pythagorean-theorem - [1]
mathsisfun.com
https://www.mathsisfun.com/pythagoras.html - [2]
khanacademy.org
https://www.khanacademy.org/math/algebra/quadratics - [2]
mathshistory.st-andrews.ac.uk
https://mathshistory.st-andrews.ac.uk/Biographies/Brahmagupta/ - [3]
exploratorium.edu
https://www.exploratorium.edu/pi/history-of-pi - [3]
mathshistory.st-andrews.ac.uk
https://mathshistory.st-andrews.ac.uk/Biographies/Archimedes/ - [4]
mathsisfun.com
https://www.mathsisfun.com/geometry/slope.html - [4]
mathshistory.st-andrews.ac.uk
https://mathshistory.st-andrews.ac.uk/Biographies/Descartes/ - [5]
khanacademy.org
https://www.khanacademy.org/math/linear-algebra/vectors-and-spaces/imaginary-and-complex-numbers/v/euler-s-formula - [5]
mathshistory.st-andrews.ac.uk
https://mathshistory.st-andrews.ac.uk/Biographies/Euler/ - [6]
tutorial.math.lamar.edu
https://tutorial.math.lamar.edu/Classes/CalcI/DefinitionOfDerivative.aspx - [6]
mathshistory.st-andrews.ac.uk
https://mathshistory.st-andrews.ac.uk/HistTopics/The_rise_of_calculus/https://mathshistory.st-andrews.ac.uk/HistTopics/The_rise_of_calculus/








0 Comments